动态规划的解题笔记(经典题打家劫舍和740.)
动态规划的解题笔记(经典题打家劫舍和740.)
定义子问题
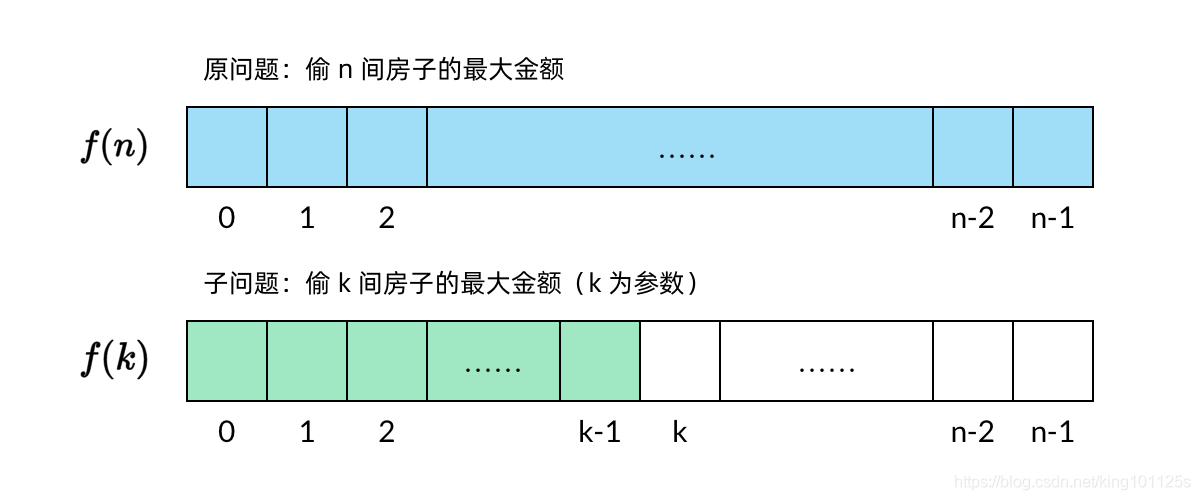
原问题是:”从全部房子中能偷到的最大金额”
把问题转换成以下,
子问题:”从k个房子中能偷到的最大金额”
cdsn博主写的很对,我也搬运一下
可以看到,子问题是参数化的,我们定义的子问题中有参数 kk。假设一共有 nn 个房子的话,就一共有 nn 个子问题。动态规划实际上就是通过求这一堆子问题的解,来求出原问题的解。这要求子问题需要具备两个性质:
- 原问题要能由子问题表示。例如这道小偷问题中,k=nk=n 时实际上就是原问题。否则,解了半天子问题还是解不出原问题,那子问题岂不是白解了。
- 一个子问题的解要能通过其他子问题的解求出。例如这道小偷问题中,f(k)f(k) 可以由 f(k-1)f(k−1) 和 f(k-2)f(k−2) 求出,具体原理后面会解释。这个性质就是教科书中所说的“最优子结构”。如果定义不出这样的子问题,那么这道题实际上没法用动态规划解。
小偷问题由于比较简单,定义子问题实际上是很直观的。一些比较难的动态规划题目可能需要一些定义子问题的技巧。
简单来说(原则):
-
原问题能用子问题表示
-
一个问题的解通过其他子问题的解求出,即偷
k-1个房子,有多少种偷法?
下面会讲到偷法。
写子问题的递推关系
我们来分析一下这道小偷问题的递推关系:
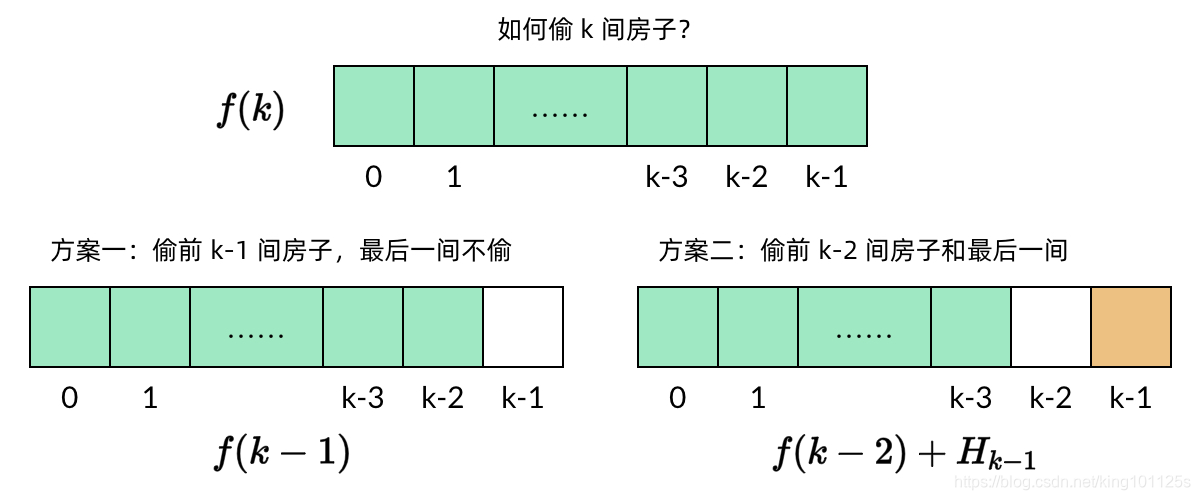
假设一共有 nn 个房子,每个房子的金额分别是 H0, H1, …,Hn-1,子问题 f(k)f(k) 表示从前 k 个房子(即 H0, H1,…Hk-1,中能偷到的最大金额。那么,偷 k 个房子有两种偷法:
- k 个房子中最后一个房子是 H(k-1)。如果不偷这个房子,那么问题就变成在前 k-1个房子中偷到最大的金额,也就是子问题 f(k-1)。
- 如果偷
k-1这个房子,那么前一个房子 H(k-2)显然不能偷,其他房子不受影响。那么问题就变成在前 k-2 个房子中偷到的最大的金额。两种情况中,选择金额较大的一种结果。
关系式 \(f(k) = {f(k-1), H(k-1) + f(k-2)}\)
在写递推关系的时候,要注意写上 k=0k=0 和 k=1 k=1 的基本情况:
- 当 k=0 时,没有房子,所以 f(0) =0。
- 当 k=1 时,只有一个房子,偷这个房子即可,所以 f(1) = H0
这样才能构成完整的递推关系,后面写代码也不容易在边界条件上出错。
确定DP数组的计算顺序
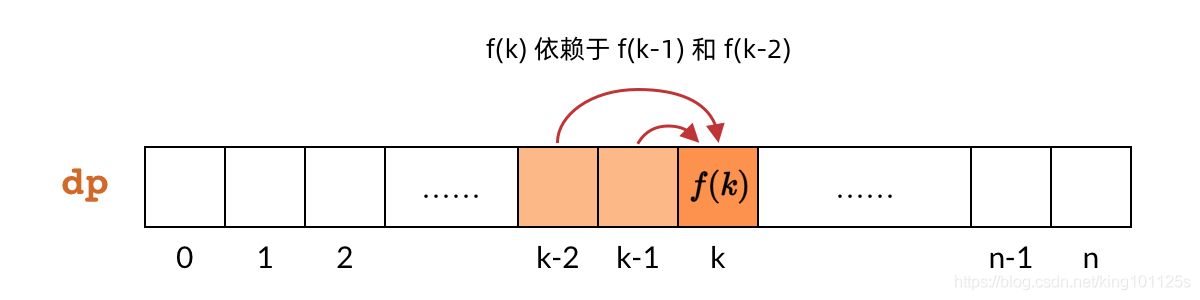
新建 DP 数组也可以叫 ”子问题数组”,因为 DP 数组中的每一个元素都对应一个子问题。如下图所示,dp[k] 对应子问题 f(k),即偷前 kk 间房子的最大金额。
那么,只要搞清楚了子问题的计算顺序,就可以确定 DP 数组的计算顺序。对于小偷问题,我们分析子问题的依赖关系,发现每个 f(k) 依赖 f(k-1) 和 f(k−2)。也就是说,dp[k] 依赖 dp[k-1] 和 dp[k-2],如下图所示。
那么,既然 DP 数组中的依赖关系都是向右指的,DP 数组的计算顺序就是从左向右。这样我们可以保证,计算一个子问题的时候,它所依赖的那些子问题已经计算出来了。
确定了 DP 数组的计算顺序之后,我们就可以写出题解代码了:
- 比较
num[i](i>2)房子和下一间房子的金额,写一个比较大小函数并返回值max() - 循环累加的金额,并用
max()赋值到新变量,为下一个比较做准备。 - 返回值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int rob(int* nums, int numsSize){
//加速运算的方法
if(numsSize == 0)
{
return 0;
}
if(numsSize == 1)
{
return nums[0];
}
//加速运算的方法
int first = nums[0], second = max(nums[0], nums[1]);
for(int i=2; i<numsSize; i++)
{
int temp = second;
second = max(first+nums[i], second);
first = temp;
}
return second;
}
int max(int a, int b)
{
return a>b?a:b;
}
相似题型分析:
740. 删除并获得点数
-
原问题:从num[i]删除并获取最大点数,即删除数组数量为i(所有)的数组值。
转换成子问题:从
i中获得最大点数f(i)
原则1:原问题能用子问题表示,i=f(i),
原则2:子问题的解是由其他子问题求出,f(i)f(i)=i*f(i)
- 写递推关系式
3.确定DP数组计算顺序
得出num[i]最大的数,新建dp数组,范围是最大的数+1,填充dp数组值。num[i]数组值为多少,就在dp数组的位置下加上num[i]的数组值。对此循环numSize,即在dp数组上累加,累加后,dp[i] 对应子问题 f(i)。最后比较dp数组累加的点数,即从i=2时累加,比较dp数组,从左到右返回dp数组里的最大值。